El juego [de azar] rey
El juego [de azar] rey
El juego [de azar] rey
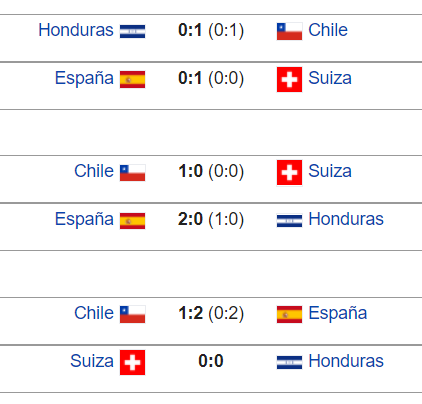
Ejemplo de tripleta intransitiva. Fase de grupos del Mundial de Sudáfrica de 2010. Chile le ganó a Suiza y Suiza a su vez le ganó a España. Si no hubiera azar en el fútbol Chile tendría que haberle ganado a España, pero perdió. De hecho, España salió campeón del mundo y Chile quedó eliminado en octavos de final.
Investigadores del Departamento de Astronomía de la Universidad de Maryland, analizaron 147 tripletas sin empates en Copas del Mundo, descubrieron que el 12% eran intransitivas. Es decir, A le ganó a B, B le ganó a C y, contrario a lo esperado a partir de los dos resultados anteriores, C le ganó a A.
“Esto parece comparativamente bajo, pero hacemos notar que incluso si los resultados de los partidos fueran completamente aleatorios, la fracción esperada sería solo del 25%”, concluyen. Anderson y Sally, autores de The Numbers Game, sugieren a partir de estas cifras que “la mitad de todos los partidos de mundiales se decide por azar, no por habilidad”.
Vota!
(1 votos, promedio: 3.00)
Loading...Fuentes
G. K. Skinner y G. H. Freeman, “Are soccer matches badly designed experiments?”, Journal of Applied Statistics, 2009, vol. 36, num. 10, pp. 1087-1095, http://arxiv.org/pdf/0909.4555v1.pdf; Christopher Anderson y David Sally, The Numbers Game: Why Everything You Know about Soccer is Wrong. Penguin, 2013.